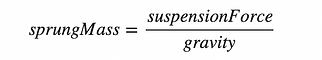Lesson 6 - Suspension and Chassis design
Welcome to the sixth lesson of SpeedScienceHQ's Physics of Racing series. In this lesson, we will explore the fundamental principles of racecar suspension and chassis design. A properly designed suspension and chassis can help a racecar maintain traction, navigate turns more efficiently, and provide a smoother ride. We will examine the different types of suspensions, how they work, and the factors that affect their performance. We will also discuss the various types of chassis designs used in racing, including their advantages and disadvantages, and how they can impact a car's performance. Join us to discover the science behind creating the perfect suspension and chassis setup for a racecar.
Racecar Suspension & Chassis Design
- Basics
Racecar suspension and chassis design play a critical role in a car's performance on the track. To design a suspension system, engineers have to take into account several factors such as the car's weight, aerodynamics, and the forces it experiences while cornering, accelerating, and braking. In this lesson, we will cover the following topics:
Types of Suspensions: There are three basic types of suspensions - independent, dependent, and semi-independent. Independent suspensions allow each wheel to move up and down independently, while dependent suspensions link the wheels together with a solid axle. Semi-independent suspensions are a combination of both.
Suspension Components: Suspension components include springs, dampers, anti-roll bars, and bushings. Springs absorb the forces of the road while dampers (or shock absorbers) control the oscillations of the spring. Anti-roll bars help keep the car level in turns, while bushings provide a cushioning effect between the suspension components and the chassis.
Suspension Geometry: Suspension geometry refers to the angles and positions of the suspension components. Camber is the angle at which the wheels tilt inward or outward, caster is the angle of the steering axis relative to vertical, toe is the angle at which the wheels point inward or outward, and ride height is the distance between the chassis and the ground.
Chassis Design: Chassis design can be broken down into three main types - monocoque, spaceframe, and tubular. Monocoque designs use the car's body to support its own weight, spaceframe designs use a lightweight framework to support the body, and tubular designs use a series of tubes to form the frame.
Stiffness and Rigidity: Stiffness and rigidity are essential to maintaining a car's performance. A stiff chassis can better control the forces acting on the suspension system, which translates into better handling and stability. Engineers can use a formula to calculate stiffness: Stiffness = Force / Deflection.
Racecar Suspension & Chassis Design
- Advanced: Hooke's Law
A suspension is essentially a damped spring producing opposing force when being compressed. Springs sustain the weight of the vehicle. Dampers oppose the spring movement, dissipating their energy and preventing them to bounce without control.
The force produced by the springs depends on the distance they are compressed and it's given by Hooke's Law:
where
K = the spring's stiffness or spring rate in N/m�/�, and
x = is the contact depth or compression distance in m�.
The force produced by the dampers depend on how fast the suspension is being compressed or elongated (contact speed), opposing the movement.
When a wheel is lifted from the ground the suspension produces no force. At the slightest contact possible it also won't produce any force. As the spring gets more compressed, more force is produced proportionally to the contact depth:
The compression limit is the suspension distance. Beyond this point the spring has reached its maximum force and cannot compress further. A hard contact with the rigid body is produced.
The slope of the force line is given by the stiffness K. The more stiffness, more steep slope.
The suspension position is the contact depth where the spring force matches exactly the force applied on the spring. In vehicles this force is typically caused by the weight supported by the wheel:
-
The more weight is loaded on a wheel, the more compressed will be its spring (suspension position visibly lower).
-
The less weight is loaded on a wheel, the less compressed will be its spring (suspension position visibly higher).
-
If the center of mass of a vehicle is moved (load, passengers...) the weight will be redistributed along the wheels and their suspensions will be compressed / elongated as result of the new weight distribution.
-
If the vehicle is accelerating, braking or cornering the weight will be temporarily shifted among the wheels, varying their suspension positions accordingly. For instance, accelerating makes a certain amount of weight (depending on the actual acceleration) to be transfered from front wheels to rear wheels. Similar effects happen when braking and cornering.
-
Aerodynamic surfaces push the vehicle down with speed, increasing the load on the wheels and compressing their suspensions accordingly.
How to calculate suspension force:
When the suspension is not moving the contact speed is 0. This happens when the vehicle is either resting, cruising at constant speed or under constant acceleration. The suspension position for a specific wheel may then be calculated as:

Advanced Suspension - The oscillating behaviour
.The suspension properties may be studied from the point of view of the oscillating behavior (Harmonic oscillator). The associated concepts are used to study the reactions of the suspension in different situations.
Given the force produced by the suspension at a specific steady state (contact speed = 0) the equivalent sprung mass value for studying that situation may be calculated as:
When the vehicle is at rest, cruising at constant speed or under constant acceleration the sum of the sprung masses of all the wheels matches the mass of the vehicle exactly.
Using the sprung mass you may calculate the natural frequency for the spring under that load. The natural frequency is the speed at which the spring can respond to changes in load:
The natural frequency defines the oscillating behavior of the suspension. A typical family car is set up to exhibit a natural frequency somewhere between 5 and 10.
The sprung mass is also used for studying the damping behavior, that is, the rate at which the suspension dissipates the energy stored at the spring. We may calculate the damping ratio for learning whether the suspension will be under-damped, over-damped or critically-damped:
A damping ratio greater than 1.0 means over-damping (sluggish suspension), a value of exactly 1.0 is critically-damped, and a value less than 1.0 is under-damped (bouncy suspension). Values for realistic vehicles are in the range of 0.2 and 0.6. The damper rate that targets a specific damping ratio may be calculated by rearranging the equation above:
In under-damped suspensions (dampingRatio<1) the frequency at which the system oscillates is different than the natural frequency:
Underdamped Frequency =
The End ->